Platonic Solids
In three-dimensional space, a Platonic solid is a regular, convex polyhedron. It is constructed by congruent regular polygonal faces with the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.
- Tetrahedron – four equilateral triangle faces
- Cube (hexahedron) – six square faces
- Octahedron – eight equilateral triangle faces
- Dodecahedron – twelve pentagon faces
- Icosahedron – twenty equilateral triangle faces
Check out these cool Animated Platonic Solids courtesy of Wikipedia!
Making Platonic Solids
I’ve enjoyed making Paper Platonic Solids for years, and on our weekend trip to Three Rivers, CA, and studio visit with my cousin Mike Perez, I learned that what I’ve been up to with paper & glue, he’s been up to with steel & arc welders!

Mike’s series is Polyhedronomics: derivatives of the regular Platonic solids in disguise. A series of 5 sculptures using one of the regular Platonic solids as the beginning framework of each piece.














It was exciting to see Mike take the beauty and simplicity of the Platonic Solids to a rich complexity in Platonic Solids in Disguise. I’m eager to see how his Octahedron and Dodecahedron develop. I hope to see the collection in a gallery show one day.


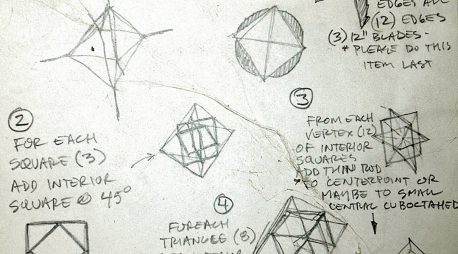
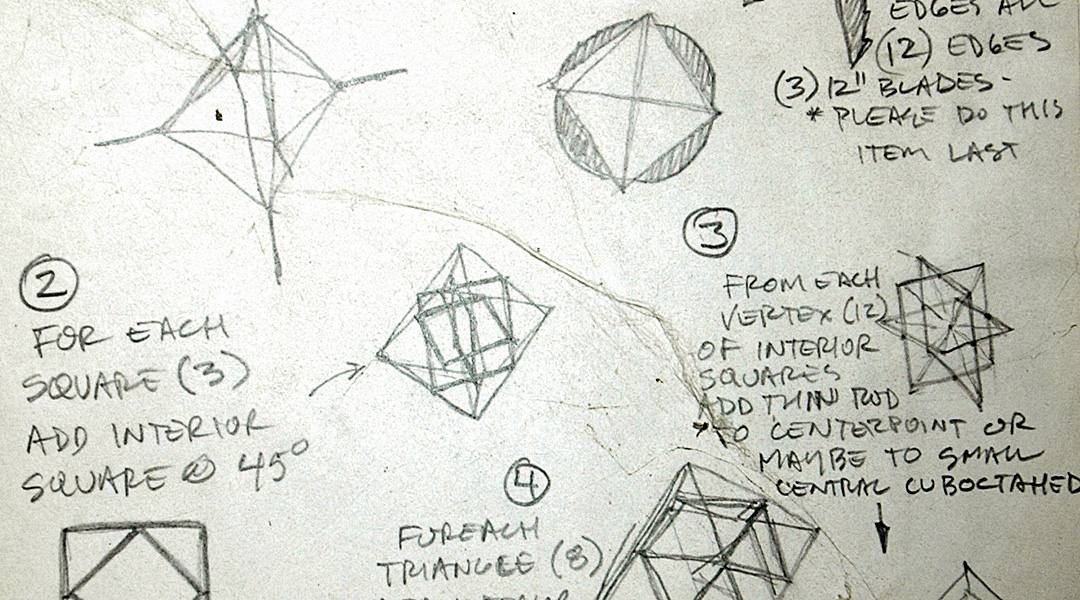
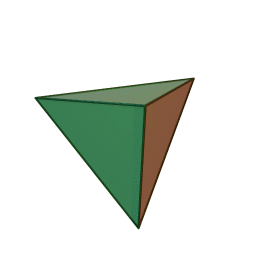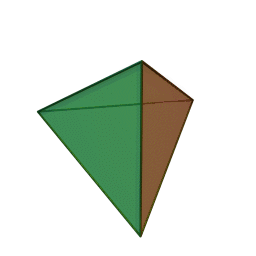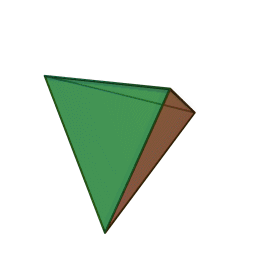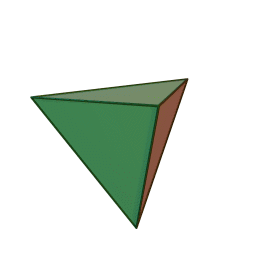
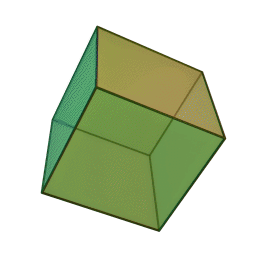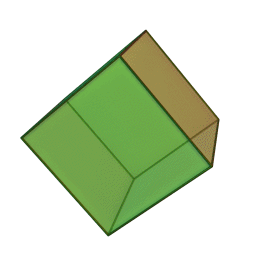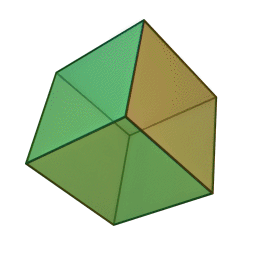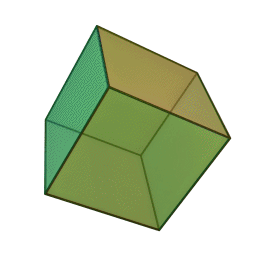
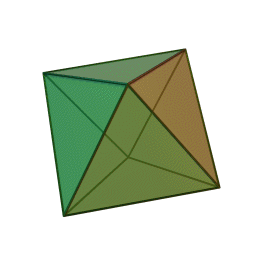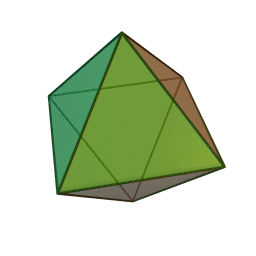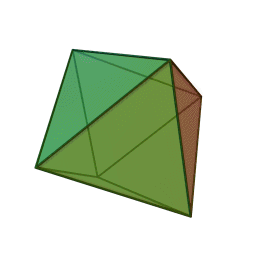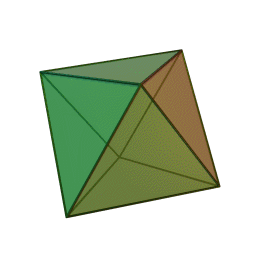
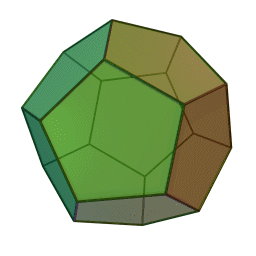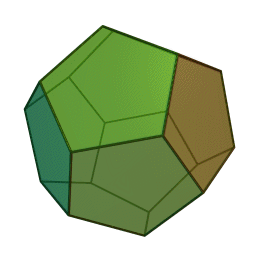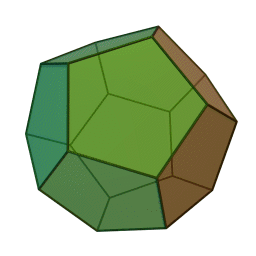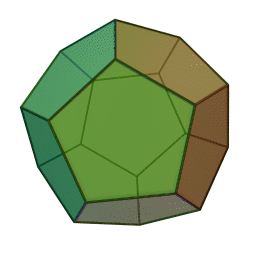





Update: Heard from Mike on Saturday that he’d just delivered his Hexahedron Hypercube for Arts Visalia’s That Extra Dimension, 2015, Invitational Sculpture & Functional Art Exhibition, July 1st – July 31st, 2015, Reception: Friday, July 3rd, 6:00 – 8:00 pm
http://artsvisalia.org/072015.php